An insight into the Gershgorin circle theorem
Eigenvalues and eigenvectors often appear in the mathematics of machine learning, in areas such as Principle Component Analysis (PCA) and Singular Value Decomposition (SVD). Eigen means “own” or “self” in German, and an eigenvector is a special linear transformation of a matrix. Assuming you more or less know what they are (if not, 3Blue1Brown’s YouTube video explains the visual interpretation really well), I’m going to explain the more niche topic of “how to find all the eigenvalues” in this short post.

The Gershgorin circle theorem
The Gershgorin circle theorem, also known as the Gershgorin disk theorem, tells you where the eigenvalues are in a complex plane.
Let’s use a simple example of a 4 by 4 matrix to illustrate the idea.
\[A = \begin{bmatrix} \alpha_{00} & \alpha_{01} & \alpha_{02} & \alpha_{03}\\ \alpha_{10} & \alpha_{11} & \alpha_{12} & \alpha_{13}\\ \alpha_{20} & \alpha_{21} & \alpha_{22} & \alpha_{23}\\ \alpha_{30} & \alpha_{31} & \alpha_{32} & \alpha_{33}\\ \end{bmatrix}\]We place the diagonal entries of this matrix in a complex plane.
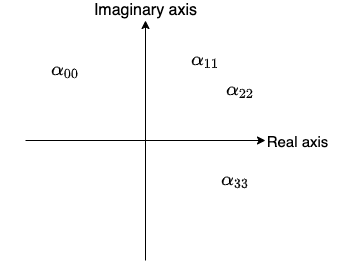
Now, calculate the sum of the absolute values of the non-diagonal entries for each row.
\[\rho_0 = |\alpha_{01}| + |\alpha_{02}| + |\alpha_{03}| \\ \rho_1 = |\alpha_{10}| + |\alpha_{12}| + |\alpha_{13}| \\ \rho_2 = |\alpha_{20}| + |\alpha_{21}| + |\alpha_{23}| \\ \rho_3 = |\alpha_{30}| + |\alpha_{31}| + |\alpha_{32}|\]Then draw a circle around each diagonal entry with radius $\rho$ as follows:
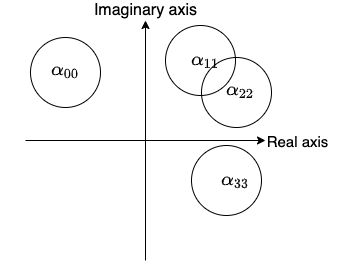
Gershgorin circle theorem basically says that all the eigenvalues of the matrix $A$ can be found in the union of these circles.
You can see that the size of the circle is based on the off-diagonal entries. If the norm of the off-diagonal entries is small, you can more accurately find the eigenvalue. It is not necessarily the case that each eigenvalue is in each circle. It could be the case that one circle contains more than one eigenvalue.
I hope this very short post gave you some insights into how to find eigenvalues using the Gershgorin circle theorem.